Creating large, intricate nets can be a cumbersome task. But similar to modular programming, the construction of CP-nets can be broken into smaller pieces by utilizing the facilities within CPN Tools for creating substitution transitions. Conceptually, nets with substitution transitions are nets with multiple layers of detail – you can have a somewhat simplified net that gives a broad overview of the system you are modeling, and by substituting transitions of this top-level net with more detailed pages, you can bring more and more detail into the model.
Substitution transitions
In hierarchical nets there is a method by which a transition can represent an entire piece of net structure, so that the net containing the transition executes as if the logic that the transition represents were physically present at the location of the transition. Such a transition is a substitution transition.
Substitution transitions add nothing fundamentally new. Everything that can be done with them can also be done by using fusion places. But like fusion places, substitution transitions add so much convenience that they can make the difference between modeling feasibility and total impossibility.
Let us consider a substitution transition named Reverse which stands for a net that is used to reverse a list of integers. A small blue tag, called a subpage tag, is associated with the substitution transition Reverse.
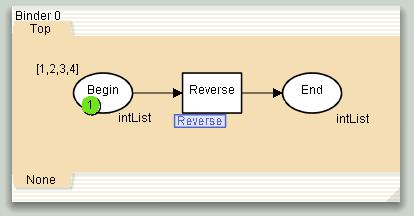
A substitution transition
Arcs surrounding substitution transitions may or may not have inscriptions. However, these inscriptions have no semantic meaning.
Subpages and superpages
A page that contains a substitution transition is called a superpage. The page named Top in the figure above is a superpage.
When a CP-net uses a substitution transition the logic that the transition represents must be kept somewhere. It is kept on a page called a subpage, and the logic on the subpage is called a subnet or a submodel.
The page named Reverse is the subpage associated with the substitution transition Reverse
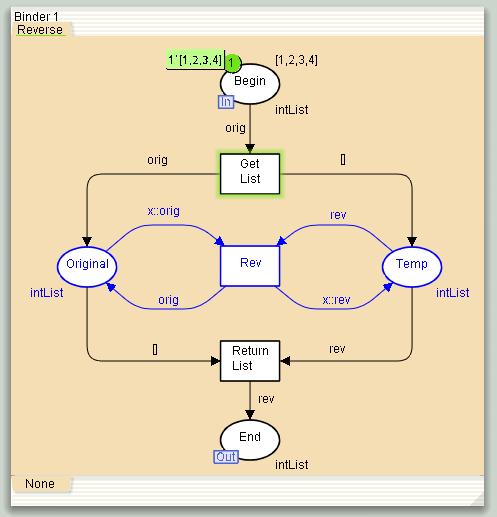
A subpage
Each substitution transition is said to be a supernode of the corresponding subpage.
The hierarchical structure of a net, i.e. the relationships between subpages and superpages, is shown in the index entry for the overview of the net. The name of a subpage is always shown below the name of its superpage, and the name of the subpage is always indented with respect to the name of the superpage.
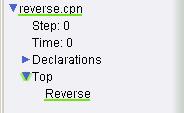
Hierarchical structure
If a subpage name is not visible in the index, click on the blue arrow next to the superpage to unfold its list of subpages.
Ports and sockets
Superpages and subpages are connected by equating places on the two pages using special-purpose fusion sets. These special fusion sets always contain only two places. A place that belongs to such a fusion set is called a port if it is on a subpage, and a socket if it is on a superpage.
Sockets
A socket is a place that is a neighbor to a substitution transition, i.e. there is always at least one arc between a substitution transition and a socket.
Places Begin and End on page Top are sockets.

Two sockets
Ports
A port-type tag is associated with each port on a subpage. Places Begin and End on page Reverse are ports.
A port
There are three kinds of port-type tags: In-tags, Out-tags, and I/O-tags.
Port/Socket assignments
Port/socket assignments are used to define how a subpage should be “glued together” with the surroundings of its supernode. Each socket must be assigned to a port on the corresponding subpage. A port with an In-tag must be assigned to a socket which is an input node (and not an output node) of the substitution transition. Analogously, an Out-tag indicates that the port must be related to a socket which is an output node (and not an input node), while an I/O-tag indicates that the socket must be both an input and output node.
Note that the arcs surrounding a port do not have to correspond to the port-type tag. For example, there may be arcs from a transition to a port that has an In-tag, i.e. the port may be an output node for a transition on the subpage even though it has an In-tag.
To learn about how port/socket assignments are indicated, read about the graphical feedback for port-type tags.
Markings of ports and sockets
Tokens that are present on a socket in a superpage are simultaneously present on the corresponding port on the subpage, and vice versa.
For example, the initial marking of the place Begin on (super)page Top is the same as the initial marking of the place Begin on the (sub)page Reverse.
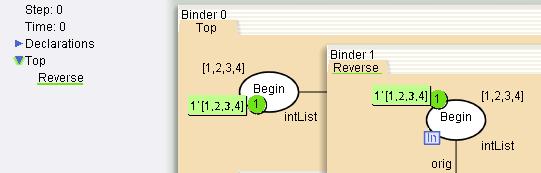
Port/socket marking
Using a subpage more than once
The real power of substitution transitions lies in the fact that a subpage need not be the value of only one substitution transition: it can be used repeatedly, as the value of any number of substitution transitions on any number of superpages.
If a subpage is the value of more than one substitution transitions, there are said to be multiple instances of the subpage. Analogously, there are also multiple instances of the places and transitions on the subpage. The marking of each instance of a subpage can be completely independent from the markings of other instances of the same subpage.
Here is a net with two instances of subpage Reverse, as indicated by the (1) and (2) following the page name. Note that the markings of the two instances of the place Begin on the page Reverse are different: they are the same as the initial markings of the corresponding sockets.
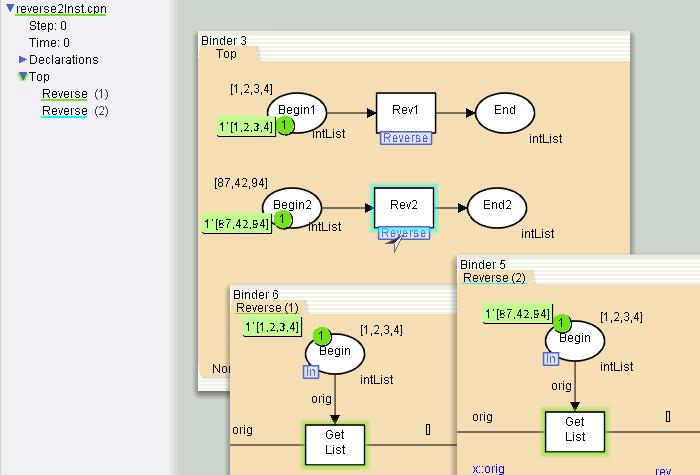
Multiple instances of a subpage
To learn about how to find out which subpage instance is associated with a substitution transition, read about the graphical feedback for subpage tags.
Help topics for Hierarchical Nets
- Bottom-up development
- Fusion places
- Hierarchy tags
- Inscriptions in hierarchical nets
- Limitations
- Redo/Undo
- Removing hierarchical constructs
- Substitution transitions
- Top-down development
To learn more about hierarchical nets you can also examine the Example nets for the Hierarchical protocol example, the Ring protocol example, or the Telephone example.
You must be logged in to post a comment.