Introduction
CPN Tools does not natively support inhibitor arcs. It is however possible to simulate the behavior of inhibitor arcs.
This can be done in at least two different ways. It can be done using lists. This way is a bit more cumbersome, but can be made to work in all cases. Simulation of inhibitor arcs can also be done using anti-places. This is a lot easier, but only works if the number of tokens is limited on the place you want to attach the inhibitor arc to.
Example

The net models a simple producer/consumer.
The producer (not modeled explicitly) sends packets onto the network.
If the consumer is ready, it can receive the packet, process it and again be ready (the blue cycle). If no packet is present on the network, the consumer can go to sleep, and wake up again (the brown cycle).
The problem is the part “if no packet is present on the network”. This is modeled using an inhibitor arc (the fat red one). Alas CPN Tools do not support this…
Using lists
One way to overcome the missing inhibitor arcs is by using lists.
Basically, one models inhibitor arcs by changing the type from e.g. T to list T, change all incoming arcs (in to the place) to add to the list, and all outgoing arcs must then remove a random element from the list (and send the list back to the place). Your inhibitor arc is then a double-arc, which removes (and again adds) the empty list.
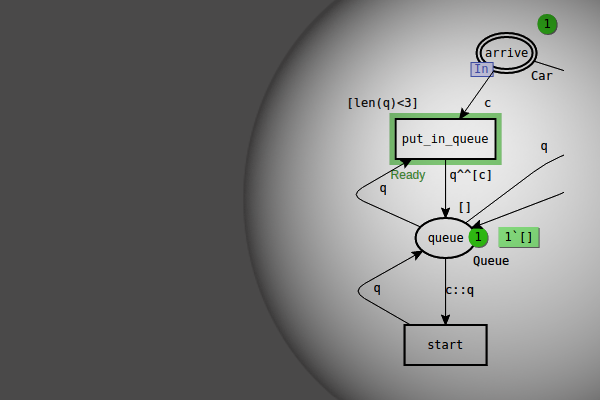
When this is done for the above example, the result is

Changes to declarations
- I have added the type
PACKAGESs, as aslist PACKAGE. - I have created a couple variables,
psandrestof the new typePACKAGEs - I have added a new function
pick, which given a list, returns a random element from the list and the rest of the list if such an element exists. Otherwise it returnsNONE. This function can be used for all types, so if you need to create an inhibitor arc using lists, you can just copy this function.
Changes to the involved place
- I change the type of the place from
PACKAGEtoPACKAGEs. - I add/change an initial marking which is now a list of tokens; in this case the original initial marking was the empty marking, and I add in stead the empty list
[]. Had the original initial marking been, e.g.,1`1++2`4, I would have changed it to[1, 4, 4].
Incoming arcs
Incoming arcs are treated just like I would for a stack.
- I change the inscription from
ptop::ps, wherepif of the typePACKAGEandpsis of the typePACKAGEs - I add a new arc in the opposite direction, with the inscription
ps
Outgoing arcs
Outgoing arcs are a bit more complicated than for queues or stacks, because I have to pick a random element.
- I change the inscription of the original from
ptops(i.e. in stead of picking one arbitrary element, I take the whole lot) - I add a new arc, which simply puts
restback to the place. This variable is of the typePACKAGEs, that is, it is the same.
Now we have two problems: the p I used originally is no longer bound from the place and the newly introduced rest is not bound either. I choose to bind both in the guard of the transition.
- I add the arc inscription
[SOME (p, rest) = pick ps]. For the transition to fire, this must evaluate to true. First, thepickfunction must returnSOME <something>, and notNONE, so ifpsis the empty list, this cannot be satisfied, which is the correct behavior. Second, I bindpto the first component thepickfunction returns, that is a random element fromps, and I bindrestto the rest of the elements.
Inhibitor arc
Finally I have to put a reasonable inscription in the inhibitor arc.
- I put the inscription
[]on the inhibitor arc - I change the inhibitor arc to a double-arc
Now the transition connected to the inhibitor-arc can only fire if there is an empty list on the involved place, which is exactly the desired behavior of an inhibitor arc.
Using Anti-places
The list-based inhibitor arc-solution is quire complex, and in some cases not needed. If the number of tokens on the involved place is bounded one can add inhibitor arcs easier by adding an anti-place and letting the inhibitor arc be a double arc, which removes (and adds) all tokens from the anti-place.
In the above example, I can see that the network can at most have 4 tokens, so this method can be used here. When this is done, I obtain:

First I have found an arbitrary bound for the involved place, in this case 5. (I could have chosen 4, 7, or 1000000 as bound as well).
I have then added an anti-place, to turn the place into a limit place, with the selected limit, as described here.
Now it is easy to add the inhibitor arc:
- I add an arc from the anti-place to the transition
- I add the inscription
5`e, where5is the limit chosen above.
If the place was bounded before, adding the anti-place has not changed its behavior, and this construction is correct.
Using a separate counter place
This solution is more general than the one using anti-places (as it works for unbounded nets) and better for timed models than the one using lists as it represents tokens individually. The basic idea is to use a separate place always keeping count of the number of tokens on the place. In a sense, this can be thought of as a anti-place where, instead of removing, we add tokens when adding tokens to the original place.
Using the same example, we get

I have added a new place Network counter of type INT with the initial marking 0. Whenever I add a token to network, I increase the value of the counter and whenever I consume a token, I decrement the value. The inhibitor arc is simply a double arc reading the value 0.
Examples
The models described in this document can be downloaded:
- the original example with no inhibitor arc behavior
- the list based inhibitor arc-construction
- the anti-place based inhibitor arc-construction
- the counter based inhibitor arc-construction
You must be logged in to post a comment.