Documentation

Function for generating values from chi-square distributions. Interface chisq(n:int) : real where n>=1. It returns a drawing from a chi-square distribution with n degrees of freedom. The sum of the squares of n independent normally distributed random variables with mean 0.0 and standard deviation 1.0 is a chi-squared distribution with n degrees of freedom. It raises Chisq exception if n<1. Characteristics Mean: n Variance: 2n […]

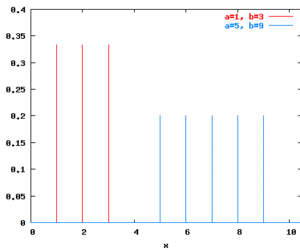
Function for generating values from discrete uniform distributions Interface discrete (a:int, b:int) : int where a<=b. Returns a drawing from a discrete uniform distribution between a and b (a and b included). Raises Discrete exception, if a>b. Characteristics Mean: (a+b)/2 Variance: ((b-a+1)^2-1)/12 Probability mass functions for discrete uniform distributions: Example discrete(1,6) Throwing a die has a discrete uniform distribution with parameters a=1 and b=6. The […]

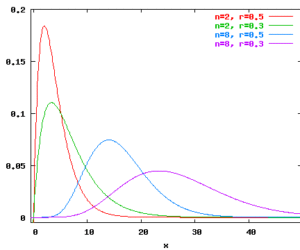
Interface erlang(n:int, r:real) : real where n>=1 and r>0.0. Returns a drawing from an n-Erlang distribution with intensity r. A drawing from an n-Erlang distribution can be derived by addition of n drawings from a exponential distribution. Raises Erlang exception, if n<1 or r<=0.0. Characteristics Mean: n/r Variance: n/r^2 Density functions for n-Erlang distributions: Example erlang(100,50.0) A shop gives each 100th customer a present. The […]

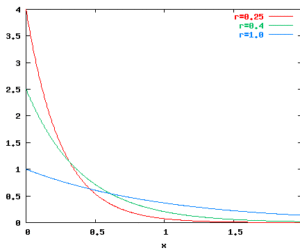
Function for generating values from exponential distributions Interface exponential(r:real) : real where r>0.0. Gives a drawing from a exponential distribution with intensity r. Raises Exponential exception, if r<=0.0. Characteristics Mean: 1/r Variance: 1/r^2 Density functions for exponential distributions: Example exponential(1.0/4.0) Customers arrive at a post office for service. The time between two arrivals has a mean of 4 minutes. The inter-arrival time has an exponential […]

Note: Introduced in CPN Tools 3.2.2. Interface gamma(l:real, k:real) : real where l,k>=0.0. Returns a drawing from a gamma distribution with parameters l and k, where l is the rate parameter (l=1.0/θ) and k is the shape parameter. Raises Gamma exception, if k<= 0.0 or l<=0.0. Related pages Random distribution functions

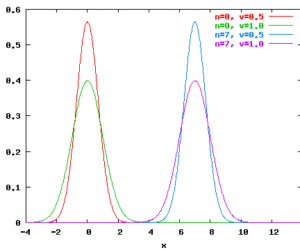
Interface normal(n:real, v^2:real) : real Returns a drawing from a normal distribution with mean n and variance v. Raises Normal exception, if v<0.0. Characteristics Mean: n Variance: v Density functions for normal distributions: Example normal(505.0,4.0) A factory produces chocolate in packages of 500 grams. The amount of chocolate in each package has a normal distribution with mean n=505.0 grams and variance v=2.0 (as v^2=4.0) grams. […]

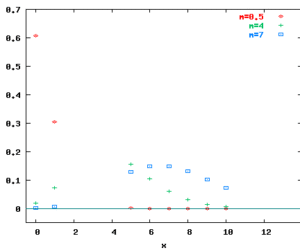
Interface poisson(m:real) : int where m>0.0. Returns a drawing from a Poisson distribution with intensity m. Raises Poisson exception, if m<=0.0. Characteristics Mean: m Variance: m Probability mass functions for Poisson distributions: Example poisson(100.0) A company has a network with a certain load. Each second an average of 100 packets is sent to the network. The number of packets arriving to the network per second […]

Note: Introduced in CPN Tools 3.4.0. Interface rayleigh(s:real) : real where s >=0.0. Returns a drawing from a rayleigh distribution with parameter s. Raises Rayleigh exception, if s<=0.0. Related pages Random distribution functions

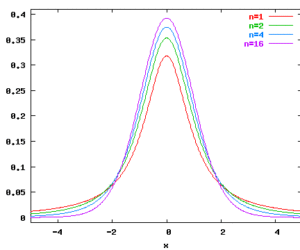
Interface student (n:int) : real where n>=1. Returns a drawing from a Student distribution (also called t distribution) with n degrees of freedom. Note that as n increases, the Student density approaches the normal density. Indeed, even for n=8, the Student density is almost the same as the normal density. Raises Student exception, if n<1. Characteristics Mean: 0 Variance: 1/n-2 Density functions for student distributions: […]

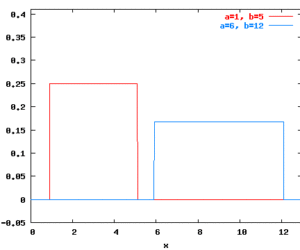
Interface uniform(a:real, b:real) : real where a<=b. Returns a drawing from a continuous uniform distribution between a and b. Raises Uniform exception, if a>b. Characteristics Mean: (a+b)/2 Variance: ((b-a)^2)/12 Density functions for continuous uniform distributions: Example uniform(1.0,10.0) A person is asked to choose a real number between 1 and 10. This random variable is uniformly distributed with parameters a=1.0 and b=10.0. Related pages Random distribution […]